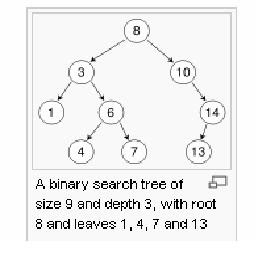
Binary Search Trees
In computer science, a binary search tree (BST) is a binary tree data structure which has the following properties:
• each node (item in the tree) has a value;
• a total order (linear order) is defined on these values;
• the left subtree of a node contains only values less than the node's value;
• the right subtree of a node contains only values greater than or equal to the node's value.
The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient.
Binary search trees can choose to allow or disallow duplicate values, depending on the implementation.
Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.
The use of bianry search tree to organize such collections of rtecords enablaes reasobale performance to be achieved both for access direclty to particular record based upon its names and for access sequentially to the entire collection in order by record’s names.
Operations on Binary Search Trees
There are four basic operation on bunary search trees: direct search, sequential search, node insertion, and node deletion.
The properties of a binary search tree simply that there is a procedure for determining whether or not a node with a given name resides in the tree and for determining whether or not a node with a given name resides in the tree and for finding that node when it exists. To find the node with name n in the binary search tree whose root node is Ri:
1. If the tree is empty, then the search terminates unsuccessfully.
2. If n= Ni, then the search terminates successfully; the sought node is R1.
3. If n < Ni, then the left subtree of Ri is searched, i.e., Ri := Left(Ri).
4. If n > Ni, then the right subtree of Ri is searched, i.e, Ri := Right(Ri).
Sequesntial search of a binary tree is accomplished by traversing the nodes of the tree in such a way that the nodes are visited in order by their names.
Inserting a new node with name n in the binary search tree rooted at Ri:
1. If the tree is empty, then the node with the name n becomes the root.
2. If n = Ni, then the insertion terminates unsuccessfully; the name is already in the tree.
3. If n < Ni, then the left subtree of Ri is searched until the appropriate position for the node is found.
4. If n > Ni, then the right subtree of Ri is searched until the appropriate position of the new node is found.
Deleting a node in the binary search tree
If the node to be deleted is a leaf, then the process is simple; the leaf is pruned nearly from the tree.
If the node to be deleted is not a leaf, then the process must do something to preserve that nodes’ subtress.
Saturday, April 26, 2008
Binary Search Tree
Posted by
igon
at
7:57 AM
![]()
Subscribe to:
Post Comments (Atom)
WELCOME!
Good day everyone!
Welcome to the coolest Blog on the WEB!
Enjoy reading great posts here...
Thanks for the visit.
Be blessed!!!
Welcome to the coolest Blog on the WEB!
Enjoy reading great posts here...
Thanks for the visit.
Be blessed!!!

No comments:
Post a Comment